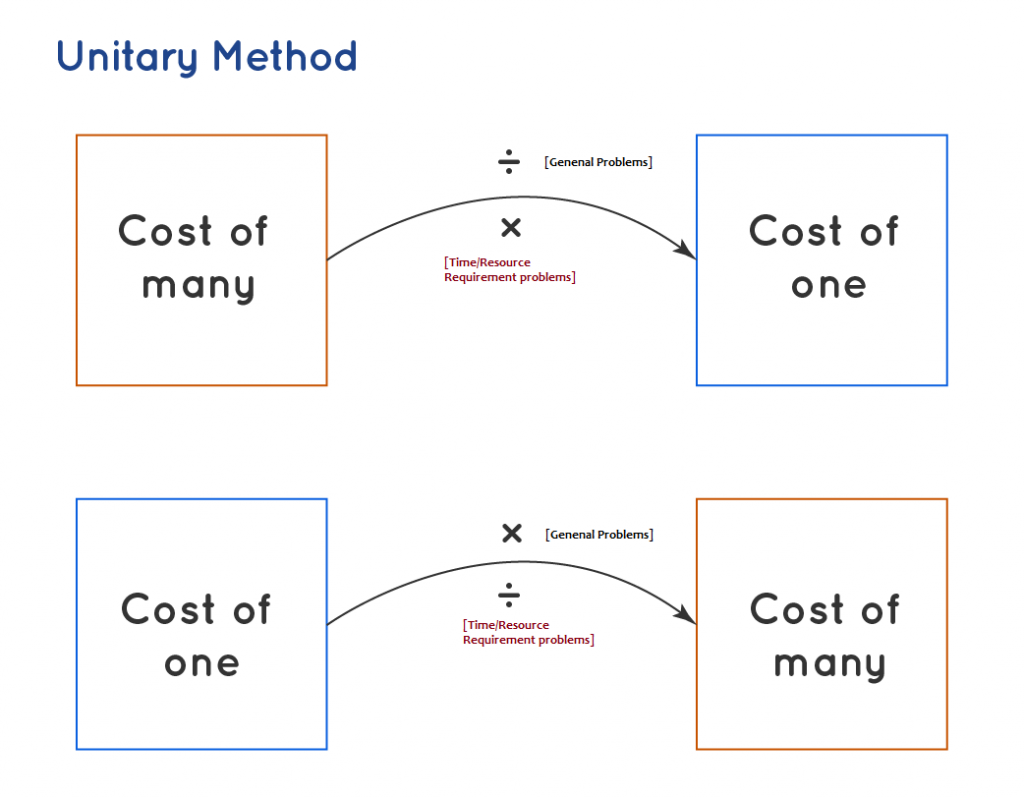
The unitary method is a mathematical problem-solving technique where the value of a single unit is found out from the value of multiple units prior to finding the necessary result. The unitary method is widely used in mathematics to solve word problems of various kinds like algebra, ratio, proportions, geometry, etc. The word unitary itself means individual or single unit.
Example’s of the Unitary Method
Let’s understand the concept and rules of the unitary method using the following example:
Example Problem: If the cost of 12 pens is $36. What is the price of 7 pens?
To solve this problem we have to first find out the price for a single unit of the pen. So we will find that by dividing 36/12=$3. So, each unit of pen costs $3. In the next step, we will find the price for 7 pens by multiplying $3 by 7 as 7*3=$21. So, the unitary method is quite simple.
Rules of Unitary Method
As shown in the above example, the problem solving using the unitary method is very simple. Simply follow the following rules
Rule 1: Keep the required answer on the right side
Always arrange the given statement in such a fashion to keep the required answer on the right side. For example, in the above example, the required answer was the price. So, you have to keep the price on the right side and solve the problem in the following fashion:
The cost of 12 pens is $36 Hence, the Cost of 1 pen=36/12=$3 (division) So, the cost of 7 pens is 7*3=$21 (multiplication)
If the above problem was modified as “How many pens can you buy with $30?” In that situation, your required answer is the number of pens. Hence you have to rearrange the statement to keep the quantity on the right side. So, the problem must be solved as follows:
$36 have the purchasing power of 12 pens Hence, $1 has the capability to purchase 12/36 number of pens (division) So, with $30 one can get (12/36)*30=10 number of pens. (multiplication)
Rule 2: Ask a question to find if you expect an increase or decrease of value when you wish to know the value of unit quantity.
In maximum of the cases, when finding the value of unit quantity the factor will decrease and thus division will happen as explained in the above examples. Means if the cost of 12 pens is $36. So, the price of 1 pen will reduce and thus division has to be performed. But there will be situations when this may not be true. The unitary method problems related time and resources usually does not follow the same. Look at the example given below:
If 12 men can do a job in 24 days, how many days will be required for 6 person to do that work?
In this problem, as 12 men can do a job in 24 days, So if the same job is required to be performed by only one man then the time required will be increased. So, in this case, multiplication needs to be performed. So your question to the statement expects an increase in the value. Hence the problem will be solved like the following:
12 men can do the job in 24 days. So, 1 man can do the same job in 12X24 days (multiplication) Hence, 6 men will do the job in (12*24)/6=48 days (division).
While working out the worksheets of the unitary method, the above two rules must be kept in mind. Refer to the Fig. 1 below:
Fig. 1: Unitary Method
Unitary Method Worksheet
I Hope, by now your understanding of the unitary method concept is clear and are in a position to solve the following unitary method problems.
Use the unitary method to find out the correct answers from the given options.
Q1. The cost of 7 toys is Rs. 315. Find the cost of 1 toy?
45
40
37
35
Q2. The cost of 12 kg sugar is Rs. 480. What will be the cost of 4 kg sugar?
80
120
140
160
Q3. A factory produces 75 masks in 5 hours. If it operates 8 hours daily, how many masks does it produce in a week?
780
840
690
920
Q4. A grocer bought 2 dozen eggs at Rs. 24 per dozen and sold them Rs. 5 per piece. How much did he earn on selling all the eggs?
72
70
68
80
Q5. A train covers 824km in 8 hours. What distance will it cover in 5 hours?
555km
525km
560km
515km
Q6. The annual rent of a building is Rs. 48000. Find the rent for 7 months?
28000
30000
24000
32000
Q7. If a quarter kg of tomato costs Rs. 10. How many rupees will 2 kg cost?
70
80
85
90
Q8. Arun earns Rs. 63000 in 3 months. How much will he earn in a year?
254000
290000
252000
3 00000
Q9. Shalini bought one dozen bananas at Rs. 60. Find the cost of one banana?
10
20
5
7
Q10. A factory manufactures 175 shirts in 5 days. How many shirts can be manufacture in 3 days?
105
95
125
110
Q2. Unitary method worksheet 2: Word problems
A. Aharsi can prepare 14 drawings in a week. So, How many drawings he can prepare in a month? If he was told to draw 21 drawings, how much time Aharsi would have taken?
B. If 15 chocolates cost Rs. 225. How many chocolates Advik can buy with Rs. 150?
C. A train travels 235 Km in 5 hours. If the distance between Howrah to Mumbai is 1880 Km, What will be the time required for a traveler to reach Mumbai from Howrah by the same train?
D. 15 students can decorate the assembly hall in 10 hours. How many hours will be required if 20 students participate in the activity? Due to urgency, the assembly hall is required in 2 hours. So how many students are required to decorate it?
E. 15 books contain 3375 pages. So, what will be the number of pages for 21 such books?
F. In the year 2020, the bus fare per 5 kilometers was Rs 15. In the year 2021, the fare has increased by Rs 1 per kilometer. Jharna wants to travel 30 km by bus. What will be her expenses for this journey?
G. 14 cows cost the same as 42 goats. The cost of one goat is 25 OMR. Firan wants to purchase 2 cows for his cultivation work. What will be his expenses?
H. A clock loses 15 seconds in 10 hours; how much does it lose in 2 days?
